7.4  Parsing a mesh

Reading all the contents of a file is straightforward, but “parsing” a file can require some effort, i.e. when you want to extract specific parts based on the structure of the contents. The following is an example of how this can be done for a certain file format that uses fixed width formatting.

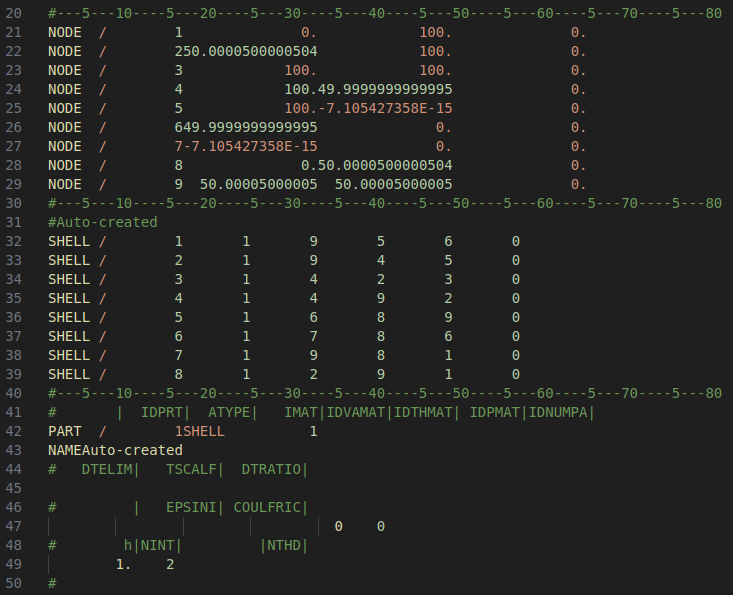
The example file describes a two-dimensional finite element mesh consisting of eight connected triangles. We are interested in computing the total area of the geometry. To do this, we first need to parse all lines starting with NODE and SHELL from the file, then compute the area of each individual triangle. All other lines in the file are not of interest, and should be ignored.

The code below initializes two empty lists: nodes and elements, then loops over each line of the file. Data is only appended to each list if a line begins with NODE or SHELL. Slicing is applied to collect only the relevant part of each line. Convince yourself about the slicing index by running for example print(str(line[6])), to see what it returns. Casting is used to specify the data type of each collected variable, and the function .strip() is used to clean up leading empty spaces (at the start) or trailing new-line characters (at the end). Note especially the order of each operation. Finally, after looping through all the lines in the file, the two lists are converted into numpy-arrays according to best practice, which enables much more efficient calculations using the stored data.

import numpy as np

nodes = []
elements = []

with open('100x100mm_8_linear_trias.pc', 'r') as file:
    for line in file:
        if line.startswith('NODE'): # Collect nodes coordinates
            NID = int(line[7:16].strip())
            NX = float(line[16:32].strip())
            NY = float(line[32:48].strip())
            NZ = float(line[48:64].strip())
            nodes.append([NID, NX, NY, NZ])
        elif line.startswith('SHELL'): # Collect element connectivity
            EID = int(line[7:16].strip())
            N1 = int(line[24:32].strip())
            N2 = int(line[32:40].strip())
            N3 = int(line[40:48].strip())
            elements.append([EID, N1, N2, N3])

np_nodes = np.array(nodes) # store gathered nodes in numpy-array
np_elements = np.array(elements) # store gathered elements in numpy-array

Since we know the x-, y- and z-coordinates of each node in every element, we can utilize linear algebra to compute the area from the vector product of the element sides. Recall that the vector product \(\mathbb{u} \times \mathbb{v}\) is a new vector \(\mathbb{w}\) (perpendicular to both \(\mathbb{u}\) and \(\mathbb{v}\)) whose magnitude \(||\mathbb{w}|| = \sqrt{w_x^2 + w_y^2 + w_z^2}\) represents the area of the parallellogram defined by \(\mathbb{u}\) and \(\mathbb{v}\) as sides. The area of a triangular element is therefore \(A_i = \frac{1}{2}||\mathbb{w}||\).

Before we can define any vectors, we need the coordinates of each node for the current element (and these are separated in two different arrays) - so we must loop over the elements. Consider n1 in the code below, which will contain the x-, y- and z- coordinates of the first node in the current element. To actually get there requires a convoluted expression consisting of multiple nested “lookup” and slicing-operations. It works by searching the np_nodes array for the row where the Node ID (column 0) matches the ID specified in element[1], and then it extracts only the coordinate columns (1, 2, and 3) from that matching row. With the exception of determining n1, n2 and n3, the following area calculations are trivial thanks to the power of linear algebra!

area = 0
for element in np_elements:
    n1 = np_nodes[np_nodes[:, 0] == element[1]][0][1:4]
    n2 = np_nodes[np_nodes[:, 0] == element[2]][0][1:4]
    n3 = np_nodes[np_nodes[:, 0] == element[3]][0][1:4]
    u = n2 - n1 # triangle edge vector 1
    v = n3 - n1 # triangle edge vector 2
    w = np.cross(u, v) # perpendicular to triangle
    area = area + 0.5 * np.linalg.norm(w)
print(area)

By combining these two snippets of code, we can iterate over all the elements in the mesh (denoted nele), determine the edge vectors \(\mathbb{u}\) and \(\mathbb{v}\) from the nodal coordinates, compute their area \(A_i\), and sum them all together for the total area \(A = \sum_i^{nele}A_i\).