Code
import numpy as np
import matplotlib.pyplot as plt
import mechanicskit as mk9.9 patch() Examples
This notebook demonstrates the patch() function for visualizing finite element meshes, truss structures, and field data.
Basic Truss Examples
Setup: Define a simple truss geometry
Code
# Node coordinates (mm)
P = np.array([[0, 0],
[500, 0],
[300, 300],
[600, 300]])
# Element connectivity (1-based node numbers)
edges = np.array([[1, 2],
[1, 3],
[2, 3],
[2, 4],
[3, 4]])
U = np.array([[ 0. , 0. ],
[-0.1984, 0. ],
[ 0.2466, 0.09 ],
[ 0.445 , -0.9116]])
U_res = np.sqrt(U[:, 0]**2 + U[:, 1]**2)Example: Basic Truss Visualization (Uniform Color)
fig, ax = plt.subplots(figsize=(8, 6))
mk.patch('Faces', edges, 'Vertices', P, 'LineWidth', 2)
ax.plot(P[:, 0], P[:, 1], 'o', color='cyan',
markeredgecolor='black', markersize=14)
ax.axis('equal')
ax.axis('off')
ax.set_title('Basic Truss')
plt.show()
Example: Per-Element Colors (Flat Mode)
Visualize element forces with flat coloring (one color per element).
# Element forces (N)
forces = np.array([6052.76, -5582.25, -7274.51, 6380.16, -9912.07])
fig, ax = plt.subplots(figsize=(8, 6))
mk.patch('Faces', edges, 'Vertices', P,
'FaceVertexCData', forces,
'FaceColor', 'flat',
'LineWidth', 3,
'cmap', 'RdBu_r') # Red for tension, blue for compression
mk.cmap('RdBu_r', label="Element forces", shrink=0.8)
ax.axis('equal')
ax.axis('off')
ax.set_title('Element Forces (Flat Colors)')
plt.show()
print(f"Force range: {forces.min():.1f} to {forces.max():.1f} N")
Force range: -9912.1 to 6380.2 NExample: Per-Vertex Colors (Interpolated Mode)
Visualize nodal temperatures with interpolated coloring.
scale = 50
P_deformed = P + scale * U
fig, ax = plt.subplots(figsize=(8, 6))
mk.patch('Faces', edges, 'Vertices', P)
mk.patch('Faces', edges, 'Vertices', P_deformed,
'FaceVertexCData', U_res,
'FaceColor', 'interp',
'LineWidth', 4,
'cmap', 'jet')
mk.cmap('jet', label="Displacement Magnitude (mm)", shrink=0.8)
ax.axis('equal')
ax.axis('off')
ax.set_title('Nodal Temperatures (Interpolated Colors)')
plt.show()
Example: Transparency (FaceAlpha)
fig, ax = plt.subplots(figsize=(8, 6))
mk.patch('Faces', edges, 'Vertices', P,
'FaceVertexCData', forces,
'FaceColor', 'flat',
'LineWidth', 4,
'FaceAlpha', 0.5)
ax.plot(P[:, 0], P[:, 1], 'o', color='red',
markeredgecolor='black', markersize=14)
ax.axis('equal')
ax.axis('off')
ax.set_title('Semi-Transparent Elements (alpha=0.5)')
plt.show()
3D Examples
Example: 3D Truss
# 3D node coordinates
P_3d = np.array([[0, 0, 0],
[500, 0, 0],
[300, 300, 0],
[600, 300, 0],
[300, 150, 400]])
# 3D element connectivity
edges_3d = np.array([[1, 2],
[1, 3],
[2, 3],
[2, 4],
[3, 4],
[1, 5],
[2, 5],
[3, 5],
[4, 5]])
# 3D element forces
forces_3d = np.array([100, -80, 50, -120, 90, -150, 110, -95, 130])
fig = plt.figure(figsize=(10, 8))
ax = fig.add_subplot(111, projection='3d')
mk.patch('Faces', edges_3d, 'Vertices', P_3d,
'FaceVertexCData', forces_3d,
'LineWidth', 2,
'cmap', 'coolwarm',
ax=ax)
ax.scatter(P_3d[:, 0], P_3d[:, 1], P_3d[:, 2],
color='yellow', edgecolor='black', s=100)
ax.set_xlabel('X (mm)')
ax.set_ylabel('Y (mm)')
ax.set_zlabel('Z (mm)')
ax.set_title('3D Truss with Element Forces')
plt.show()
Surface Element Examples
Example: 2D Surface Elements (Triangles)
# Triangular mesh vertices
vertices_2d = np.array([[0, 0],
[1, 0],
[0.5, 0.866],
[1.5, 0.866],
[1, 1.732]])
# Triangle connectivity
faces_2d = np.array([[1, 2, 3],
[2, 4, 3],
[3, 4, 5]])
# Per-element colors
face_colors = np.array([0.2, 0.5, 0.8])
fig, ax = plt.subplots(figsize=(8, 6))
mk.patch('Faces', faces_2d, 'Vertices', vertices_2d,
'FaceVertexCData', face_colors,
'FaceColor', 'flat',
'EdgeColor', 'black',
'LineWidth', 2,
'cmap', 'plasma')
ax.plot(vertices_2d[:, 0], vertices_2d[:, 1], 'ko', markersize=8)
ax.set_aspect('equal')
ax.set_title('2D Triangular Elements')
plt.colorbar(ax.collections[0], ax=ax, label='Element Value')
plt.show()
Example: 3D Surface Element (Quad with Transparency)
# 3D quad vertices
vertices_3d_surf = np.array([[0, 0, 0],
[1, 0, 0],
[1, 1, 0],
[0, 1, 0]])
# Quad face
faces_3d_surf = np.array([[1, 2, 3, 4]])
fig = plt.figure(figsize=(8, 6))
ax = fig.add_subplot(111, projection='3d')
mk.patch('Faces', faces_3d_surf, 'Vertices', vertices_3d_surf,
'FaceColor', 'red',
'FaceAlpha', 0.6,
'EdgeColor', 'black',
'LineWidth', 2,
ax=ax)
ax.scatter(vertices_3d_surf[:, 0], vertices_3d_surf[:, 1], vertices_3d_surf[:, 2],
color='blue', s=100)
ax.set_xlabel('X')
ax.set_ylabel('Y')
ax.set_zlabel('Z')
ax.set_title('3D Quad Surface (Transparent)')
plt.show()
Advanced Examples - Quad Meshes and Field Visualization
Setup: Define a quad mesh geometry
Code
# More complex mesh for advanced examples
P_quad = np.array([[0, 0],
[3, 0],
[3, 1.2],
[0, 1.2],
[0.7, 0],
[1.6, 0],
[2.5, 0],
[3, 0.5],
[2.3, 1.2],
[1.5, 1.2],
[0.6, 1.2],
[0, 0.5],
[0.55, 0.4],
[1.45, 0.6],
[2.4, 0.45]])
nodes_quad = np.array([[1, 5, 13, 12],
[12, 13, 11, 4],
[5, 6, 14, 13],
[13, 14, 10, 11],
[14, 15, 9, 10],
[6, 7, 15, 14],
[7, 2, 8, 15],
[15, 8, 3, 9]])Example: Quad Element Mesh with Labels
fig, ax = plt.subplots(figsize=(10, 6))
# Draw mesh with cyan faces
mk.patch('Faces', nodes_quad, 'Vertices', P_quad,
'FaceColor', 'cyan',
'EdgeColor', 'black',
'EdgeAlpha', 0.3,
'LineWidth', 1.5,
ax=ax)
# Plot nodes
ax.plot(P_quad[:, 0], P_quad[:, 1], 'ok', markerfacecolor='black', markersize=16)
# Label nodes
for i in range(len(P_quad)):
ax.text(P_quad[i, 0], P_quad[i, 1], str(i+1),
color='w', fontsize=8, ha='center', va='center')
# Label elements at their centroids
for iel in range(len(nodes_quad)):
element_nodes = nodes_quad[iel] - 1 # Convert to 0-based
xm = np.mean(P_quad[element_nodes, 0])
ym = np.mean(P_quad[element_nodes, 1])
ax.text(xm, ym, str(iel+1), fontsize=9, ha='center', va='center')
ax.axis('equal')
ax.set_title('Quad Element Mesh with Labels')
plt.show()
Example: Displacement Field Visualization
# Create synthetic displacement field (simulating FEM results)
np.random.seed(42)
u_flat = np.zeros(2 * len(P_quad))
# Simulate bending: displacement increases with x, varies with y
for i in range(len(P_quad)):
x, y = P_quad[i]
u_flat[2*i] = 0.15 * x * (1 + 0.3 * y) # x-displacement
u_flat[2*i+1] = -0.05 * x**2 / 9 # y-displacement
# Convert to nodal displacement array (n_nodes, 2)
U = np.column_stack([u_flat[0::2], u_flat[1::2]])
# Compute displacement magnitude at each node
UR = np.sqrt(np.sum(U**2, axis=1))
# Scale factor for visualization
scale = 1.0
fig, ax = plt.subplots(figsize=(10, 6))
# Draw deformed mesh with displacement magnitude colors
mk.patch('Faces', nodes_quad, 'Vertices', P_quad + U * scale,
'FaceVertexCData', UR,
'FaceColor', 'interp',
'EdgeColor', 'black',
'EdgeAlpha', 0.5,
'LineWidth', 1.0,
'cmap', 'jet',
ax=ax)
ax.axis('equal')
ax.set_title(f'Displacement Field, scale: {scale}')
plt.colorbar(ax.collections[0], ax=ax, label='Displacement Magnitude')
plt.show()
print(f"Displacement range: {UR.min():.4f} to {UR.max():.4f}")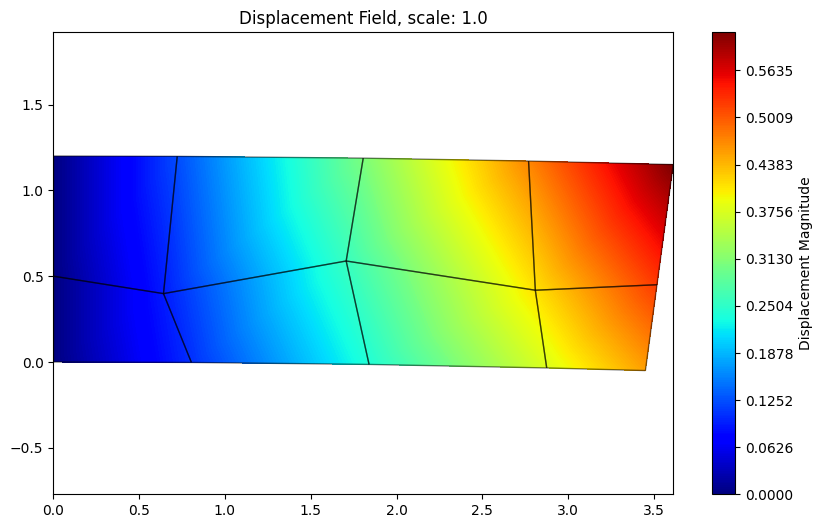
Displacement range: 0.0000 to 0.6140Example: Element Stress Field
# Create synthetic stress data (one value per element)
element_stresses = np.array([150, -80, 200, -120, 180, 90, -150, 110])
fig, ax = plt.subplots(figsize=(10, 6))
# Draw mesh with per-element colors
mk.patch('Faces', nodes_quad, 'Vertices', P_quad,
'FaceVertexCData', element_stresses,
'FaceColor', 'flat',
'EdgeColor', 'black',
'LineWidth', 2,
'cmap', 'RdBu_r', # Red for tension, blue for compression
ax=ax)
# Plot nodes
ax.plot(P_quad[:, 0], P_quad[:, 1], 'ok', markerfacecolor='yellow',
markeredgecolor='black', markersize=10)
ax.axis('equal')
ax.set_title('Element Stress Field (Flat Colors)')
plt.colorbar(ax.collections[0], ax=ax, label='Stress (MPa)')
plt.show()
print(f"Stress range: {element_stresses.min():.1f} to {element_stresses.max():.1f} MPa")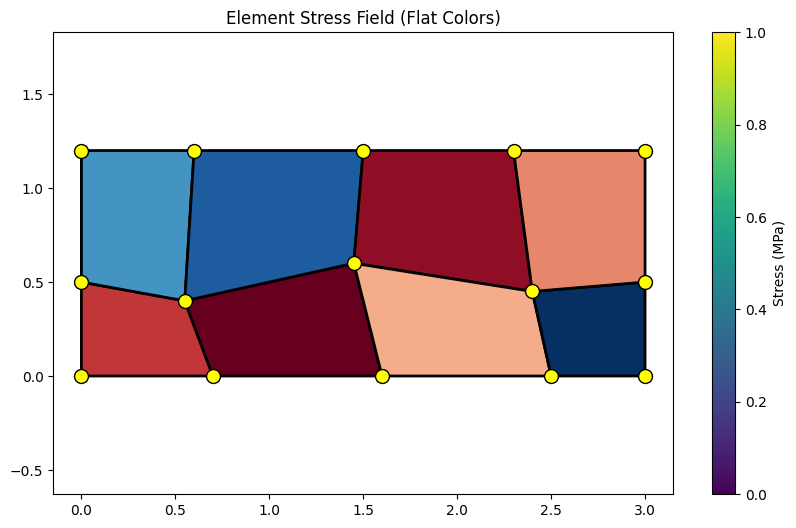
Stress range: -150.0 to 200.0 MPaExample: Temperature Field (Interpolated)
# Create synthetic temperature data (one value per node)
node_temps_quad = np.zeros(len(P_quad))
for i in range(len(P_quad)):
x, y = P_quad[i]
# Temperature increases from left to right
node_temps_quad[i] = 100 * (x / 3.0) + 20
fig, ax = plt.subplots(figsize=(10, 6))
# Draw mesh with interpolated nodal temperatures
mk.patch('Faces', nodes_quad, 'Vertices', P_quad,
'FaceVertexCData', node_temps_quad,
'FaceColor', 'interp',
'EdgeColor', 'black',
'LineWidth', 1.5,
'cmap', 'hot',
ax=ax)
# Plot nodes
# ax.plot(P_quad[:, 0], P_quad[:, 1], 'ok', markerfacecolor='cyan',
# markeredgecolor='black', markersize=10)
ax.axis('equal')
ax.set_title('Temperature Field (Interpolated Colors)')
plt.colorbar(ax.collections[0], ax=ax, label='Temperature (°C)')
plt.show()
print(f"Temperature range: {node_temps_quad.min():.1f} to {node_temps_quad.max():.1f} °C")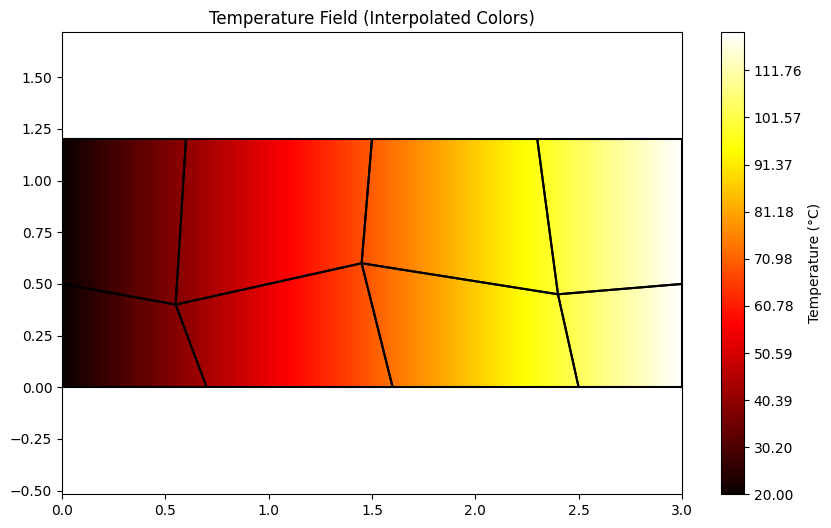
Temperature range: 20.0 to 120.0 °CExample: Displacement Comparison (Multiple Scales)
fig, axes = plt.subplots(1, 3, figsize=(16, 5))
collections = []
for idx, scale in enumerate([0.5, 1.0, 2.0]):
ax = axes[idx]
# Original mesh (light gray)
mk.patch('Faces', nodes_quad, 'Vertices', P_quad,
'FaceColor', 'white',
'EdgeColor', 'gray',
'EdgeAlpha', 0.3,
'LineWidth', 1.0,
ax=ax)
# Deformed mesh
P_def = P_quad + U * scale
pc = mk.patch('Faces', nodes_quad, 'Vertices', P_def,
'FaceVertexCData', UR,
'FaceColor', 'interp',
'EdgeColor', 'black',
'EdgeAlpha', 0.2,
'LineWidth', 1.5,
'cmap', 'viridis',
ax=ax)
collections.append(pc)
ax.axis('equal')
ax.set_title(f'Scale: {scale}')
# Add shared colorbar
# fig.colorbar(collections[0], ax=axes.ravel().tolist(), label='Displacement Magnitude', pad=0.02)
mk.cmap('viridis', label="Displacement Magnitude", shrink=0.8)
plt.suptitle('Displacement Field at Different Scales', fontsize=14)
plt.tight_layout()
plt.show()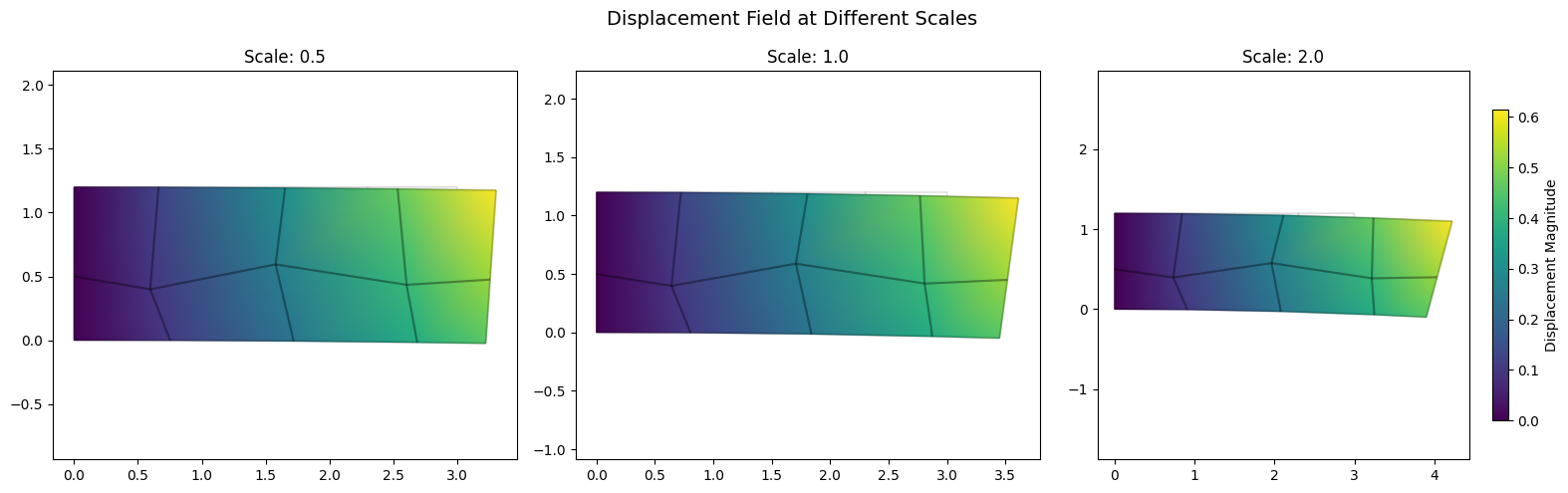
Example: FaceAlpha Variations
fig, axes = plt.subplots(1, 3, figsize=(15, 5))
for idx, alpha in enumerate([0.3, 0.6, 1.0]):
ax = axes[idx]
mk.patch('Faces', nodes_quad, 'Vertices', P_quad,
'FaceVertexCData', element_stresses,
'FaceColor', 'flat',
'FaceAlpha', alpha,
'EdgeColor', 'black',
'LineWidth', 2,
'cmap', 'plasma',
ax=ax)
# ax.plot(P_quad[:, 0], P_quad[:, 1], 'ok', markerfacecolor='white',
# markeredgecolor='black', markersize=8)
ax.axis('equal')
ax.set_title(f'FaceAlpha: {alpha}')
plt.suptitle('Face Transparency Variations', fontsize=14)
plt.tight_layout()
plt.show()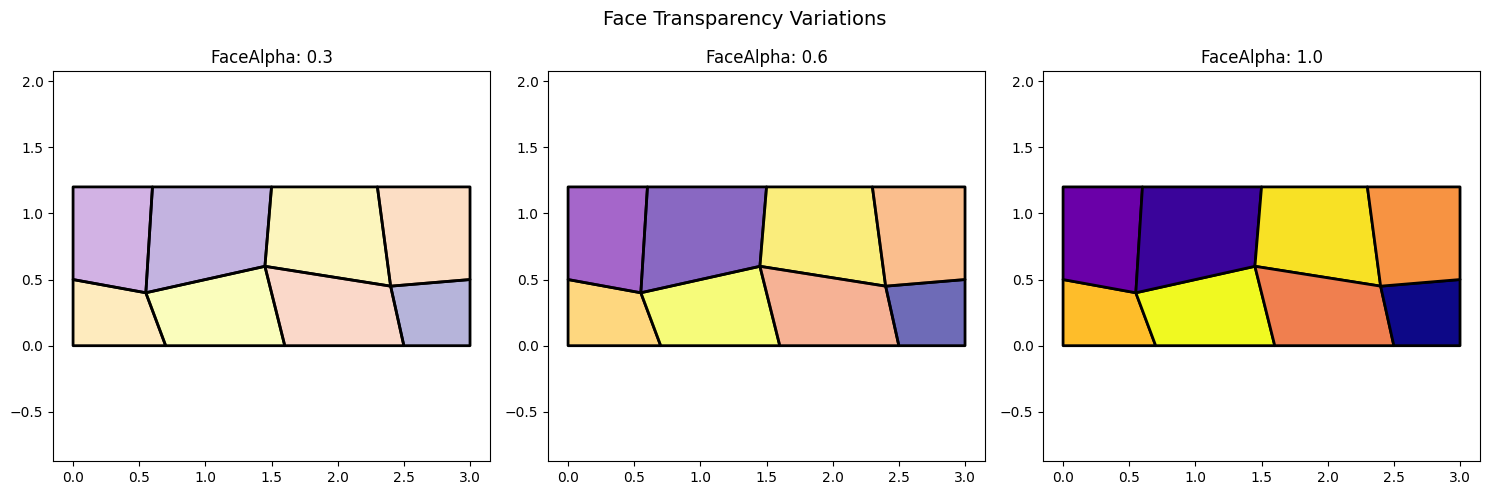
Summary
The patch() function provides flexible visualization for FEM:
Key Parameters:
- Faces: Element connectivity (1-based node numbers)
- Vertices: Node coordinates
- FaceVertexCData: Data for coloring (per-element or per-node)
- FaceColor: Color mode (
'flat','interp', or explicit color) - FaceAlpha: Transparency (0.0 to 1.0)
- EdgeColor: Edge color
- LineWidth: Edge thickness
- cmap: Colormap name (e.g.,
'viridis','hot','RdBu_r')
Color Modes:
'flat': One color per element (use with per-element data)'interp': Interpolated colors (use with per-node data)
Typical Use Cases:
- Element forces/stresses: Use
FaceColor='flat'with per-element data - Nodal displacements/temperatures: Use
FaceColor='interp'with per-node data - Deformed shapes: Add displacements to vertices:
P + U * scale